વ્યુત્પન્ન અને વિભેદક વચ્ચેનો તફાવત

વ્યુરીવેટિવ વિ વિભેદક

વિભેદક કેલ્ક્યુલેશનમાં, ડેરિવેટિવ અને ફંક્શનની વિભેદકતા નજીકથી સંકળાયેલો છે પરંતુ તેનો અર્થ ખૂબ અલગ છે, અને ભિન્ન કાર્યવાહીથી સંબંધિત બે મહત્વપૂર્ણ ગાણિતિક પદાર્થોનું પ્રતિનિધિત્વ કરવા માટે વપરાય છે.

ડેરિવેટિવ્ઝ શું છે?

ફંક્શનની ડેરિવેટિવ્ઝ તેના ઇનપુટ ફેરફારો તરીકે ફંક્શન વેલ્યુમાં ફેરફાર કરે છે તે દરને માપે છે મલ્ટી-ચલ કાર્યોમાં, કાર્ય મૂલ્યમાં ફેરફાર સ્વતંત્ર ચલોના મૂલ્યોના ફેરફારની દિશા પર આધારિત છે. તેથી, આવા કિસ્સાઓમાં, ચોક્કસ દિશા પસંદ કરવામાં આવે છે અને તે કાર્ય ચોક્કસ દિશામાં અલગ પડે છે. તે ડેરિવેટિવને દિશાસૂચક વ્યુત્પન્ન કહેવાય છે. આંશિક ડેરિવેટિવ્ઝ એક ખાસ પ્રકારનું દિશાશીલ ડેરિવેટિવ્ઝ છે.

વેક્ટર મૂલ્યવાળા કાર્યનું ડેરિવેટિવ f ની મર્યાદા તરીકે વ્યાખ્યાયિત કરી શકાય છે

જ્યાં પણ તે પૂર્ણપણે અસ્તિત્વમાં હોય ત્યાં. જેમ પહેલાં સૂચવ્યા મુજબ, આ આપણને વેક્ટરના દિશા સાથે f વેક્ટરની સંખ્યા યુ નો વધારો કરવાની દર આપે છે. એક-મૂલ્ય કાર્યવાહીના કિસ્સામાં, તે વ્યુત્પત્તિશાસ્ત્રની જાણીતી વ્યાખ્યાને ઘટાડે છે,

ઉદાહરણ તરીકે,

દરેક જગ્યાએ ભિન્નપાત્ર છે, અને ડેરિવેટિવ એ મર્યાદાની બરાબર છે,

, જે

બરાબર છે. કાર્યોના ડેરિવેટિવ્સ જેમ કે

સર્વત્ર અસ્તિત્વ ધરાવે છે તેઓ અનુક્રમે કાર્યો

બરાબર છે

આ પ્રથમ વ્યુત્પન્ન તરીકે ઓળખાય છે. સામાન્ય રીતે કાર્યનું પ્રથમ ડેરિવેટિવ્ઝ f એફ ⁽¹⁾ દ્વારા સૂચવે છે. હવે આ નોટેશનનો ઉપયોગ કરીને, ઉચ્ચ ઓર્ડર ડેરિવેટિવ્સને વ્યાખ્યાયિત કરવું શક્ય છે.

એ બીજું હુકમ દિશાત્મક વ્યુત્પન્ન છે, અને n ^મી વ્યુત્પન્ન દ્વારા f ⁽ⁿ⁾ દરેક માટે n,

, n ^મી ડેરિવેટિવ્ઝ નિર્ધારિત કરે છે.

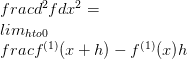
તફાવત શું છે?

વિધેયના વિભેદક સ્વતંત્ર ચલ અથવા ચલોમાં ફેરફારોના સંદર્ભમાં કાર્યમાં ફેરફારનું પ્રતિનિધિત્વ કરે છે. સામાન્ય ચલણમાં, એક જ ચલ f એક ચલના x માટે, ક્રમ 1 ડીએફ દ્વારા આપવામાં આવેલ

દ્વારા આપવામાં આવે છે. આનો અર્થ એ થાય છે કે x (એટલે ​​કે x) માં અજાણ્યા પરિવર્તન માટે, ત્યાં f ⁽¹⁾ (x <) ડી x ફેરફાર એફ. મર્યાદાઓનો ઉપયોગ નીચે પ્રમાણે આ વ્યાખ્યા પ્રમાણે કરી શકે છે. ધારેલા Δ

x એક મનસ્વી બિંદુ x અને Δ f પર x માં ફેરફાર છે કાર્યમાં અનુરૂપ ફેરફાર f તે બતાવ્યું છે કે Δ f = f (1) ⁽ x) Δ x + ε, જ્યાં ε છે ભૂલ હવે, મર્યાદા Δ x → 0 Δ ^{f /} Δ _{x =} એફ (1) ( ^x ) (વ્યુત્પન્નની અગાઉની કરેલી વ્યાખ્યાની મદદથી) અને આમ, Δ x → 0 ε / ^Δ x = 0.તેથી, તારણ કાઢવું ​​શક્ય છે કે, Δ _{x → 0} ε = 0. હવે, denoting Δ x → 0 Δ f ડી તરીકે f અને Δ x → 0 Δ x તરીકે ડી x તફાવતની વ્યાખ્યા સખત મેળવવામાં આવે છે ઉદાહરણ તરીકે, કાર્યનું વિભેદક છે

બે કે તેથી વધુ વેરિયેબલ્સના કાર્યોના કિસ્સામાં, ફંક્શનની કુલ વિભેદક સ્વતંત્ર ચલોના દરેક દિશામાં તફાવતોના સરવાળો તરીકે વ્યાખ્યાયિત થયેલ છે. ગાણિતિક રીતે, તે

તરીકે વર્ણવી શકાય છે

વ્યુત્પન્ન અને વિભેદક વચ્ચે શું તફાવત છે?

• ડેરિવેટિવ્ઝ ફંક્શનના ફેરફારના દરને દર્શાવે છે, જ્યારે વિભેદક ફંક્શનના વાસ્તવિક પરિવર્તનને દર્શાવે છે, જ્યારે સ્વતંત્ર ચલને બદલીને આધિન હોય છે.

• ડેરિવેટિવ્ઝ

દ્વારા આપવામાં આવે છે, પરંતુ દ્વારા વિભેદક રૂપે આપવામાં આવે છે ભલામણ લિંકિંગ અને એમ્બેડિંગ વચ્ચેનો તફાવત સૂચિ અને અરેલી યાદી વચ્ચે તફાવત સ્થાનિક અને વૈશ્વિક ચલો વચ્ચેનો તફાવત