બાયનોમિયલ અને સામાન્ય વિતરણ વચ્ચેનો તફાવત

બાયનિયલ વિ સામાન્ય વિતરણ

સંભવિત રેન્ડમ વેરિયેબલ્સનું વિતરણ આંકડાઓના ક્ષેત્રમાં એક મહત્વપૂર્ણ ભૂમિકા ભજવે છે. તે સંભાવના વિતરણ પૈકી, દ્વિપદી વિતરણ અને સામાન્ય વિતરણ એ વાસ્તવિક જીવનમાં સૌથી વધુ સામાન્ય રીતે બનતું હોય છે.

દ્વિપદી વિતરણ શું છે?

બાયનોમિયલ વિતરણ એ રેન્ડમ વેરિએબલ X, ને અનુરૂપ સંભાવના વિતરણ છે, જે સ્વતંત્ર હા / ના પ્રયોગોના મર્યાદિત ક્રમ ની સફળતાઓની સંખ્યા છે જેમાંની પ્રત્યેક સંભાવના ધરાવે છે સફળતા પૃષ્ઠ X, ની વ્યાખ્યાથી તે સ્પષ્ટ છે કે તે એક સ્વતંત્ર રેન્ડમ વેરિયેબલ છે; તેથી દ્વિપદી વિતરણ પણ અલગ છે.

વિતરણને X ~ B (n, પૃષ્ઠ) તરીકે ઓળખવામાં આવે છે જ્યાં n પ્રયોગોની સંખ્યા છે અને p સફળતાની સંભાવના છે સંભાવના સિદ્ધાંત મુજબ, અમે તે જાણી શકીએ કે B (n, p) સંભાવના સમૂહ કાર્યને અનુસરે છે

આ સમીકરણમાંથી, તે આગળ અનુમાનિત કરી શકાય છે કે X, E (X) = np અને X નું અંતર >, વી (X) = np (1- પૃષ્ઠ).

ઉદાહરણ તરીકે, એક સિક્કો 3 વખત ઉતરવાની રેન્ડમ પ્રયોગ વિચારો. એચ મેળવવાની સફળતાને વ્યાખ્યાયિત કરો, ટી મેળવવાની નિષ્ફળતા અને રેન્ડમ વેરિએબલ

X પ્રયોગમાં સફળતાની સંખ્યા તરીકે. પછી X ~ B (3, 0. 5) અને X દ્વારા આપવામાં આવેલ સંભાવના સમૂહ કાર્ય. તેથી, ઓછામાં ઓછા 2 એચ ની પ્રાપ્તિની સંભાવના P (

X ≥ 2) = P (X = 2 અથવા X = 3) = P (< X = 2) + P (X = 3) = 3 સી ² (0.5 ₂ ) (0. 5 ¹ ) + ³ C ³ (0.25 ₃ ) (0.5 ^{0) = 0. 375 + 0. 125 = 0. 5. સામાન્ય વિતરણ શું છે?} સામાન્ય વહેંચણી સંભાવના ઘનતા કાર્ય દ્વારા નિર્ધારિત સતત સંભાવના વિતરણ છે,

પરિમાણો

વ્યાજની વસ્તીનું સરેરાશ અને પ્રમાણભૂત વિચલન દર્શાવે છે. જ્યારે

વિતરણ પ્રમાણભૂત સામાન્ય વિતરણ કહેવાય છે.

આ વિતરણને સામાન્ય કહેવામાં આવે છે કારણ કે મોટા ભાગની કુદરતી ઘટના સામાન્ય વિતરણને અનુસરે છે. ઉદાહરણ તરીકે, માનવ વસ્તીના IQ ને સામાન્ય રીતે વહેંચવામાં આવે છે. જેમ જેમ ગ્રાફ પરથી જોવામાં આવે છે તે અર્થહીન છે, મધ્યમ અને ઘંટ આકારનું સપ્રમાણ છે. સરેરાશ, સ્થિતિ અને સરેરાશ સમકક્ષ હોય છે. વક્ર હેઠળનો વિસ્તાર, આપેલ સ્થિતિને સંતોષવા, વસ્તીના ભાગને અનુરૂપ છે.

અંતરાલ

,

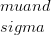
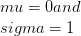
માં વસ્તીના ભાગો લગભગ 68 છે.2%, 95. 6% અને 99. 8% અનુક્રમે.

બાયનોમિયલ અને નોર્મલ ડિસ્ટ્રીબ્યુશન વચ્ચે શું તફાવત છે?

બાયનોમિયલ ડિસ્ટ્રિબ્યુશન એક સ્વતંત્ર સંભાવના વિતરણ છે જ્યારે સામાન્ય વિતરણ સતત એક છે.

દ્વિપદી વિતરણની સંભાવના સમૂહ વિધેય છે

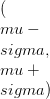
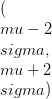
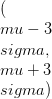
, જ્યારે સામાન્ય વિતરણની સંભાવના ઘનતા કાર્ય

• બાયનોમિયલ ડિસ્ટ્રિબ્યુશન ચોક્કસ શરતો હેઠળ સામાન્ય વિતરણ સાથે અંદાજીત છે, પરંતુ અન્ય કોઈ પણ રીત નથી.